Geometry

Geometry on the GMAT is very basic and the questions relate just to lines, triangles, circles, and other relevant concepts. So you only need to know a few fundamental definitions and formulas.

Brandon's Tip

Diagrams are a big part of the geometry portion of the exam. Keep in mind when dealing with diagrams that:

• All diagrams in the problem solving questions on the GMAT are to scale, unless otherwise noted by the question.

• This means that you can eliminate a lot of choices simply by looking at the diagram and estimating what you see in terms of length.

Lines and Angles

We will begin by reviewing lines and angles.

As we know, a line is a one-dimensional object. It has no width, and is infinitely long. A line segment is part of a straight line, and has two endpoints. Typically, a line is named for its end points: AB. The midpoint of the line is the point on the line segment that divides the line in two equal parts.

In the above example, A and B are the endpoints. M, the midpoint, is in the exact middle of line segment AB.

If we know that the distance between AM is 6, then the distance between MB is also 6. This means that the total distance of line AB is 12.

We know that an angle is formed whenever two lines, or line segments, intersect at a certain point. This point is the vertex of the angle, and the angle is measured in degrees.

There are four common types of angles.

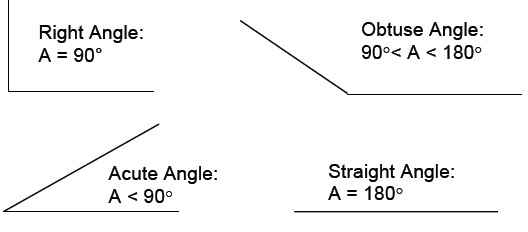
A right angle is exactly 90 degrees. An acute angle is anything less than 90 degrees, while an obtuse angle is greater than 90 degrees but less than 180 degrees. A straight angle is 180 degrees.

Lines are perpendicular if they are at 90-degree angles to each other.

When two angles added together measure 180 degrees, then the lines that make up the angles are called supplementary. If the angles measure 90 degrees, the corresponding lines are complementary.

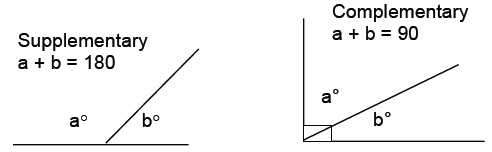
As can be seen from the examples above, when a line goes through an angle, it splits it into two smaller angles. If the split is equal, then the line is said to bisect an angle. A line that splits a 90-degree angle into two 45-degree angles is known as bisecting that angle.

Two intersecting lines create vertical angles, which are the opposite angles formed at the point of intersection. In the example below, w and y are vertical angles, as are x and z. This means x = z and w = y, and you already know that a straight line has 180º. Therefore:

w + x = y + z and

w + z = x + y and

all of the equation equals 180 degrees

If two parallel lines are intersected by a third line, which is called a transversal, the two parallel lines will intersect that third line at the same angle, as can be seen below.

In the example above, we see that a and e are equal to each other. Also, since a = c and e = g, then a = c = e = g while b = d = f = h.

Coordinate Geometry

The next concept that we will look at here is slopes. When we talk about a slope, we are talking about how steeply a line goes up or down. If a line gets higher as you move to the right, then the slope is positive. Conversely, if a line gets lower as it goes to the right, then it has a negative slope.

We can find the slope of a line using the equation:

The rise is the difference between the y-coordinate values of the two points on the line, while the run is the difference between the x-coordinates on the lines. Let's look at an example below.

What is the slope of a line with two end points at (2, 1) and (3, 6)?

Therefore, the slope is 5

Remember that a line that passes through the origin also gives you coordinates (0,0) that you can use to find slope. However, not all of the questions will give you the coordinates of a line, and you will have to figure out the slope using nothing but an equation.

All we have to do is turn the equation into y = mx + b, where m is the slope of the line and b is the y-intercept. The y-intercept is the point at which the line crosses the y axis. The value of the x coordinate at this point is always zero. For example, if you are given an equation of a line as follows:

2y - 8x - 10 = 0

We first convert the equation into the y = mx + b form by moving everything but the term y to the right side of the equation, and then divide all terms by 2.

2y = 8x + 10

y = 4x + 5

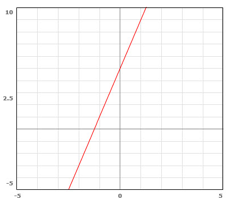
m = 4 and b = 5

Then we know that the slope of the line is 4 and the y-intercept is 5, as shown on the graph below.

Ø More Practice from the GMAT® Review 13th Edition: Questions 7, 28, 61, 202, 206

Triangles

We all know what a triangle is and how it looks, but there are a few more things we need to learn about triangles for the GMAT.

First, remember the rule that helps when figuring out the angles of a triangle: The sum of the interior angles of any triangle is 180 degrees.

Each interior angle in a triangle is supplementary to an adjacent exterior angle. The degrees of the exterior angle are then equal to the sum of the measures of the two non-adjacent, interior angles.

Confusing? Let's look at an example to help clarify this.

In this figure, the interior angles are a, b, and c, while d is the exterior angle. Looking at the three interior angles, a + b + c = 180 degrees, and since d is supplementary to c,

d + c = 180. Therefore, d + c = a + b + c and d = a + b. That means that d is equal to the sum of the two remote angles in the triangle: a and b.

Let's look at a brief equation for this:

If a = 45 and b = 90, then 45 + 90 = d, and d = 135. Therefore the angle is 135°.

The altitude of a triangle is the distance between the vertex and the side opposite the vertex. This can be inside, or even outside, the triangle.

Let's look at two examples of the triangle vertex, inside and outside.

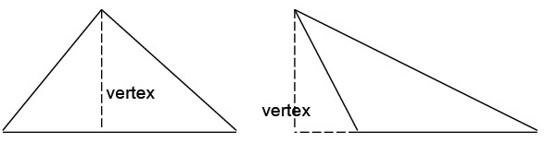
The sides of a triangle are very important. They allow us to figure out the area of the triangle when we do not have all of the information at our disposal. The length of each side of a triangle is less than the sum of the lengths of the other two sides, and greater than the positive difference of the lengths of the other two sides. This can be seen in the following equations:

b + c > a > b – c

a + b > c > a – b

a + c > b > a – c

Area

Knowing this, we can begin to figure out the area of a triangle.

The area of a triangle can be figured out with the following formula:

A = (½b × h)

where A = area, b = base and h = height.

If a triangle has a base length of 6 and an altitude (vertex) height of 3, then we have an area as follows:

A = ½ (6 × 3)

A = ½ × 18

A = 9

If we are dealing with a right angle triangle, then we can use the following formula to calculate the area:

A = ½ L₁ × L₂

L₁ and L₂ are always the legs that come out from the right angle. If their value is 6 and 21, respectively, then we can figure out the area of the triangle.

A = ½ (6) × 21

A = 3 × 21

A = 63

Perimeter

When perimeter is talked about in terms of triangles, it means the distance around the triangle. This means that the perimeter is equal to the sum of the lengths of the sides.

Here is an example:

a = 5, b = 12, c = 13

Perimeter = 5 + 12 + 13

Perimeter = 30

Isosceles and Equilateral Triangles

An Isosceles Triangle is a triangle with two sides of equal length, called the legs, while the third side is the base. As a result of the legs being the same length, the two legs on opposite sides of each other have the same angle.

In this triangle, b = c.

The other type of triangle is the Equilateral Triangle. These triangles have three sides of equal length, and three 60-degree angles.

a = b = c = 60 degrees

Right-angle Triangles

Right angles are the most recognizable triangles in geometry. The longest side of the right angle triangle is called the hypotenuse (a), while the other two sides are the legs (b and c), as mentioned in the previous example.

To calculate the area of a triangle, we can use one of the most famous mathematical equations in history: the Pythagorean Theorem.

This theorem dictates that the square of the hypotenuse is equal to the sum of the squares of the other two sides. Expressed as an equation, it reads:

a² = b² + c²

Let's look at an example of this for a better understanding of how the equation is used.

What is the length of the hypotenuse if the legs are of lengths 11 and 12?

a² = 11² + 12²

a² = 121 + 144

a² = 265

a = 16.27

You can see that sometimes the Pythagorean Theorem can be difficult to calculate. The good news is that the GMAT likes to test certain special right triangles repeatedly. If you can memorize the patterns and be on the lookout for them during the test, you won't have to do any calculations. These special right triangles are:

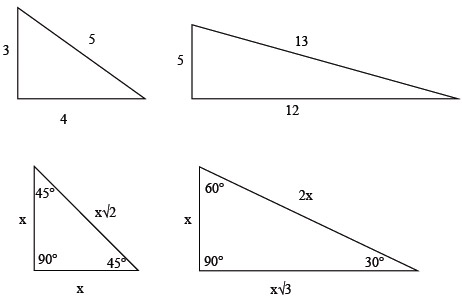
For that GMAT, that is about all we need to know about triangles. It is important to remember the differences between triangles, as well as how to find their areas and perimeters.

Only a few more sections and we will be done with geometry!

Ø More Practice from the GMAT® Review 13th Edition: Questions 75, 92, 206, 211, 228

Polygons

"Polygon" is a Greek word. Poly- means many, while -gon means angle. A polygon is a "closed" figure (all the lines connect) with straight-line segments for sides. This means that the perimeter of a polygon is the sum of the lengths of its sides.

In the example above, we can calculate the perimeter as follows:

A + B + C + D + E

So, if B = E, A = D, and B = 2, A = 3 and C = 4, then the total perimeter is:

3 + 2 + 4 + 3 + 2 = 14

The diagonal of the polygon is a line segment connected to two nonadjacent vertices. The dotted lines in the image below are examples of diagonals in a polygon. If all the sides are of equal length and the interior angles are equal, then the polygon is regular. Otherwise it is irregular.

Polygons have different names, depending on the number of sides they have. If it has three sides, it is called a triangle. If it has four sides, it is a quadrilateral. If it has five sides, it is a pentagon. If it has six sides, it is a hexagon. Triangles and quadrilaterals appear most frequently on the GMAT.

The interior and exterior angles of a polygon can easily be found by simply dividing the polygon into triangles. See below for an example:

From the previous chapter, we already know that the sum of the interior angles of a triangle is 180 degrees. Since there are three triangles whose interior angles add up to 180 degrees, the sum of the interior angles in the polygon is 3 x 180 degrees, or 540 degrees.

Let's look at another example:

In the example above, what is the sum of the angles if the polygon is divided into sections with three interior lines?

Dividing the polygon into sections with three interior lines creates four triangles. Therefore, the total sum of the angles is 180 x 4 = 720 degrees.

Quadrilaterals

Quadrilaterals are the most important aspect of geometry that appears on the GMAT, since they are by far the most frequently encountered concept on the test.

A quadrilateral, as we mentioned above, is a four-sided polygon, where the sum of the interior angles equals 360 degrees in total.

The two most common forms of quadrilaterals are squares and rectangles. A rectangle is a quadrilateral with four equal right angles, with the opposite sides of the rectangles equal in length. A square is a rectangle of four equal sides and angles.

Calculating the area of quadrilaterals, is easy. To find the area of a rectangle, simply multiply the length of the rectangle by the width (A = L x W), while the area of a square is its side squared, since all sides are of equal length (A = s²). Let's look at a few examples:

What is the area of this rectangle?

A = L × W

A = 19 × 14

A = 266

What is the area of this square?

A = s²

A = 13²

A = 169

Ø More Practice from the GMAT® Review 13th Edition: Questions 62, 78, 104, 121, 147

Circles

Many of the questions that you will see related to geometry have to do with circles. Thankfully, circles are pretty easy to understand.

Defining a circle is a bit harder than simply looking at it. In layman's terms, if all points on a plane from a certain point are of the same distance, then you have a circle. This point is the center of the circle, and all circles are labeled for their center point. The diameter of a circle is a line that connects two points of a circle and passes through the center point. The radius is a line segment from the center to the edge of the circle and is always one-half the length of the diameter.

Central angles are formed by the radii coming out from the center of the circle.

A tangent of a circle is a line that touches only one point on the circle and runs perpendicular to it.

Now we get to one of the most important pieces of information related to a circle: Pi (or "π"). The circumference of a circle is the distance around a circle. Pi is the ratio of a circle's circumference to its diameter. The value of Pi is 3.1415926… and the decimal places never, ever end - Pi is the longest non-repeating number in the universe. Thankfully, just using 3 will be enough for your GMAT calculations, but keep in mind that it is actually a little more than 3. Since Pi is equal to the ratio of the circumference to the diameter, the formula to find the circumference is C = πd or C = 2πr.

Before moving on to arcs and areas, let's just draw a circle and figure out some of the stuff we have just talked about here.

o = center of the circle r = radius line p = tangent d = diameter line

Now, the arc of a circle is the portion of the circumference of a circle. A major arc is an arc of a circle having measure greater than or equal to 180 degrees, while a minor arc is an arc of a circle having measure less than or equal to 180 degrees. If the arc is exactly half the circumference, then it is a semi-circle. Let's look at three examples.

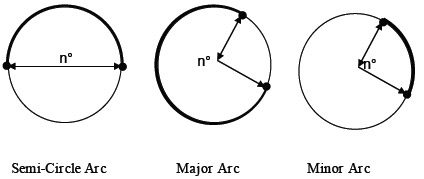
To find the length of the arc with a central point, we use the formula:

Let's look at an example.

What is the length of the arc XYZ?

Since we know that the length of the radius is 14, we can figure out the circumference.

C = 2(π)r

C = 2(3) × 14

C = 6 × 14

C = 84 (plus a little bit more)

We know the angle is 72 degrees, which means it is 72 out of 360 degrees or:

72 / 360 = 1 / 5

This means that the length of the arc is one-fifth the circumference or:

1/5 × 87.92

The equation for the area of a circle also uses Pi in the formula Area = (pi)r². Let's find out the circumference and area of the circle below:

Since we know the diameter and the radius, it is easy to figure out the circumference and the area.

Circumference = π × d

C = 3.14 × 12

C = 37.68

Area = π × r²

A = 3.14 × 6²

A = 3.14 × 36

A = 113.04

There we have it – the area and the circumference of the circle.

Ø More Practice from the GMAT® Review 13th Edition: Questions 36, 69, 175, 213

Multiple Figures

One aspect of geometry that you may not be familiar with is the concept of multiple figures. You will probably see multiple figures on your test, albeit not many of them.

Multiple figures are combinations of shapes. For example, you may find that the hypotenuse of a triangle is the side of a rectangle. Since you will be required to find the area of a particular shape, you need an eye for shapes.

Here's a sample question for a better understanding of this.

If ABCD is a rectangle, what is the perimeter of the polygon BEFC?

To figure this out, we have to look at the shapes inside the rectangle. We can clearly see a right angle triangle to the left.

Since we know that for right angled triangles, a² = b² + c², we can figure out one side of the polygon:

a² = 8² + 3.5²

a² = 64 + 12.25

a² = 76.25

a = 8.73

Now we know that one side of the polygon is 8.73. Since the triangle on the other side is the same shape, this means that the three sides of the polygon are 8.73, 8.73, and 11. To figure out the top side of the polygon, we use simple math.

11 – 3.5 – 3.5 = 4

Now we have all sides of the polygon, so the perimeter is:

a + b + c + d = 4 + 8.5 + 8.5 + 11

= 32

Other types of multiple figures:

• A circle is inscribed in a polygon (an inscribed figure)

• A circle is circumscribed around a polygon (a circumscribed figure)

Here are two examples of this:

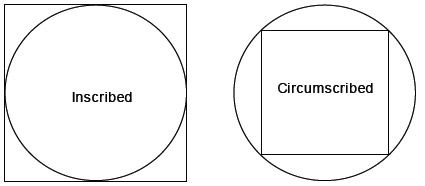
How do we figure out the perimeter of the square if we only know the circumference or diameter of the circle? Well, it is actually pretty easy. Let's look at an example.

The area of the circle above is 36(π). What is the perimeter of the square?

We know that the area of a circle is A = (π)r². So if the area here is 36(π), then we need the square root of 36, which is 6.

Now that we know the radius, we can find the diameter, which is 6 × 2 = 12.

The diameter is 12, and since this is a square, all sides are equal. The diameter equals one side; therefore, the perimeter is:

12 + 12 + 12 + 12 = 48

We could also use the same information to find the area of the square:

Diameter of the circle = 12

Area of Square = 12²

Therefore, the area of the square is 144.

Now, what about when we are dealing with a circumscribed figure? Let's try an example to figure it out.

If the circumference of the square is 8, what is the area of the circle?

First we find the length of each side of the square: 8 / 4 = 2

Notice that the diagonal of the square is also the diameter of the circle.

Our next step is to use the Pythagoras theorem to find the diagonal.

The diagonal is the square root of (2² + 2²) which equals √8.

Therefore the circle has a diameter of √8 (or 2√2 if you just used the memorized patterns from the special right triangle) and a radius of √8 / 2. We get the area of the circle by using the equation:

Area of circle =

The important thing to remember when you are working with multiple figures is to get accustomed to viewing the object within the figure. This should help you to begin to figure out how everything goes together. The above is a perfect example of this.

These are the primary shapes that you will have to deal with, and knowing your areas and perimeter formulas from previous chapters will help greatly in figuring out the answers to these questions.