The Three Techniques You Should Know
Some questions are not what they seem! Many times, there are quicker ways of getting the answer to a GMAT math question than actually going through the usual (and often much longer) steps required to solve the problem as stated in the question. The following are the three basic techniques that you should use for solving GMAT math questions:
- Backsolving
- Assigning values
- "Drawing" the questions (for word problems)
We'll start with a brief discussion of each technique and follow up with some practical applications and practice problems to show you the technique in action. Once you understand how each one works, we'll explain which techniques work best with the standard question types. Spending time understanding how to match techniques with question types now will ensure that you'll have one more step to breeze through during the actual test.
1. Backsolving
Backsolving is the first technique that we'll review. This technique is most effective for questions that have a clearly stated equation that might be difficult to solve when using standard methods (complex fractions and exponents are two examples). Instead of digging in to the ugly equation, you'll essentially work around it. This technique involves testing the answer choices provided to you for a given question. Basically, you'll select one of the five answer choices and then plug that corresponding value into the question to see if the answer is correct. If it's not correct, you quickly eliminate that choice and pick another one.
The great part about this technique is that there are only five possible choices. You can usually narrow your choices down somewhat based on the equation or the possible choices. Even if you have no idea at all, you still have a 20 percent chance of getting the right answer when you pick one choice at random! Of course, you'll know that this technique has worked if the choice correctly solves the math problem. This is a simple and effective technique for maximizing your use of time during the GMAT.
Brandon's Tip
An additional time-saver: if the answer choices are concrete values (meaning not fractions, decimals, percents, or ratios), try the middle value, choice (C), first. Since the answer choices for GMAT math questions are given in ascending order, you will probably be able to determine whether you should next try values larger or smaller than the middle value. If that first value is right, move on to the next question. If the first value is wrong but you know to go higher or lower from that point, you've still effectively narrowed your choices down from five to two – and the chance that your total guess answer will be right goes from 20 percent to 50 percent. It's techniques like this that will raise your score to the next level.
Here's backsolving in action:
What is the value of x if:
A. -2
B. -1
C. 0
D. 1
E. 2
Since 0 is often an easy value to plug in, and it just happens to be choice C, let's try that first. Solving for x = 0 gives us:
Choice (C), x = 0 is correct. Sure, you could have gone through the process of cross-multiplying these complex fractions and solving for x. In this case, that option would have taken you longer and also introduced the possibility of making a computational error that would have led you to the wrong value in the end.
Let's try another one.
Which x value results in the lowest value for y in the following equation?
A. x = 2
B. x = 4
C. x = 7
D. x = 10
E. x = 11
In this case, answer C might not be the best place to start. Because you are looking for the lowest value of y, solving for answer C won't tell you anything. You are comparing the answers to each other. Since they are sequential, start with the highest or lowest and compare what happens to y as you change the value of x. Let's start with x = 2.
Now let's increase the value of x to 4.
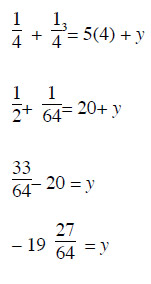
As you can see, the value of y has decreased. You can continue to solve for the remaining choices, but you can probably tell that as the value of x increases, the value of y continues to decrease. Therefore, choice E (x = 11) is correct.
Backsolving isn't useful for all question types, but recognizing the times when it is your best option will be a big help during the actual test. In this particular question, you may have been able to tell that 5x was the most influential factor on y because it gets subtracted from the left side of the equation. The left side will always be positive, so you want 5x to be as large as possible to make y negative. You could have selected choice E immediately and moved on. However, if you aren't comfortable with that estimation, backsolving is a great tool.
Ø More Practice from the GMAT® Review 13th Edition: Questions 51, 55, 72, 74, 83
2. Assigning Values
The next technique for handling GMAT math questions is similar to backsolving in that you are trying to find the answer without directly solving the question. Assigning values is something that many people do as a natural part of their routine when standard problem solving doesn't work or will be too time-consuming. What is useful about this technique is recognizing that for some types of problems it's easier to skip the initial problem solving altogether and go directly to assigning values.
Basically, you'll assign specific values to undefined terms in these questions. That will allow you to perform a simple calculation and then look at the answer choices to see which one makes sense. For example, if the question asks about integers, pick a few strategically-chosen integers (maybe a negative integer, a positive integer, and zero) and plug them into the question. If the question is asking about fractions of some quantity, choose a quantity that is a common denominator of the fractions so that they're easier to deal with.
By seeing the result that you get with each value assigned, you'll have a much better idea of which choice is correct. This technique should make working with variables and unknowns much easier. With practice, you'll get better at knowing which values to use for different questions. Assigning values will not directly give you an answer but will help you understand the question better and make choosing an answer easier.
Here's a good example of a question stem that lends itself to assigning values:
If x and y are odd integers, which of the following is an even integer?
A. x (x + 6)
B. 3x + 7y
C. (x + 4) (y - 6)
D. xy + 6
E. x (y - 4)
Of course, you could simplify some of these by multiplying through the parentheses and grouping like variables, but assigning values makes quick work of these choices. The question stem offers a simple set up – x and y are odd integers. Let's choose the easiest ones to plug in: x=3 and y=5. Assigning these values yields:
A. 27
B. 44
C. -7
D. 21
E. 3
The only value that's even is (B), 9+35=44. This type of question should be one to solve quickly so that you can move on. Saving time on questions like these will give you the time cushion you need in case you run into a really difficult question later in the test.
To make sure that you're comfortable with this technique, let's try it out with another question stem that involves number properties but is a little more difficult. This is a classic question type where assigning values will help to narrow down the choices:
If n/4 is an even integer, what is the remainder when n is divided by 8?
A. 0
B. 1
C. 2
D. 3
E. 4
There are a few ways that this problem could be approached – we're going to go through the simplest one. You know that n/4 is an even integer. That means that n divided by 4 is an even number that has no remainder. You may intuitively realize that n must be a multiple of 4, but we can work through it to identify WHICH multiples of 4 might work. First, you would assign values to n:
n=2 gives you 2/4 = 1/2 (not an integer)
n = 4 gives you 4/4 = 1 (an ODD integer)
n = 8 gives you 8/4 = 2 (an EVEN integer)
n = 16 gives you 16/4 = 4 (an EVEN integer)
Once you've established that n needs to be a multiple of 8, you may intuitively know the answer due to number properties. We can confirm this idea by testing these values. Divide by 8 to find the remainder for both:
n=8: 8/8 = 1 (remainder 0)
n=16: 16/8 = 2 (remainder 0)
The number of values assigned initially is really an arbitrary number. You should substitute as many as it takes for you to feel comfortable with the numbers that result, but keep in mind that you do have a time constraint. If you have assigned multiple values already and don't think you are closer to an answer, make an educated guess and move on. Remember that the question may be experimental and not even count, and the next question may be easier for you to answer.
Ø More Practice from the GMAT® Review 13th Edition: Questions 14, 18, 26, 31, 43, 84, 90, 103, 123, 141, 149
3. Drawing the Question
If a picture is worth a thousand words, then drawing your GMAT questions may save you thousands of seconds.
The third technique may seem a little more obvious than the first two. Whenever you come across a lengthy word problem and you find yourself having a hard time making sense of what it's saying, it's time to draw it out. Make a simple diagram for what you're given in the question and for what you're being asked. This will help you understand what the question is asking and will save you valuable time in the long run.
Here are some examples of question types where drawing might help:
• Trains/planes/vehicles traveling in the same or opposite directions
• Work problems
• Set problems
• Distance problems
Ø More Practice from the GMAT® Review 13th Edition: Questions 2, 8, 41, 84, 91, 93, 134
When to Use Each Technique
Now that you understand these three techniques, the next important step is to know when to employ these tactics. What should you be looking for when you look at the question? When is each technique useful?
When to use backsolving:
• Questions with clear numerical values given in the answer choices (If the answers include variables or indefinite terms such as "can't be determined", then backsolving won't work, because you can't substitute to confirm your answer)
• Equations with ugly fractions or exponents
• Equations with multi-digit computations
• Questions that include special symbols or functions that are defined by the question (not typical math functions or operations)
When to use assigning values:
• Generalized number problems that include variables or undefined parameters
• Questions about percents of a whole, where you can start with 100 (for percents), or for fractions involving many different denominators, you can use a common multiple
• Questions about odd and even, prime numbers, or other number properties
When to draw:
• Complex word problems
• Motion problems
• Problems that describe a physical set up
As you practice, you'll become better at quickly identifying which technique to use. Remember that the goal is to find the correct answer in the least amount of time possible, not to demonstrate your mathematical prowess by solving everything the hard way!